《七巧板 HD》遊戲介紹
有時候會想要找一些簡單的手機遊戲給父母玩,讓他們動動腦,又能打發無聊時間,
這時簡單的益智遊戲就很適合,像七巧板這類中國人發明的經典遊戲。
※小豪的媽媽則是超愛數獨
簡單的七片木板,卻可以拼出幾乎無窮無盡的圖形,
然而這類的遊戲就很適合不喜歡玩複雜遊戲的朋友。
看是等垃圾車時、飯後不想坐著想站著時,都很適合拿出來玩。
今天要介紹的是手機上一款七巧板遊戲,叫做《七巧板 HD》(Tangram),是由「Pocket Storm」所推出的遊戲。
遊戲有分「常規」與「大師」大師兩種,建議可以先從常規入手。
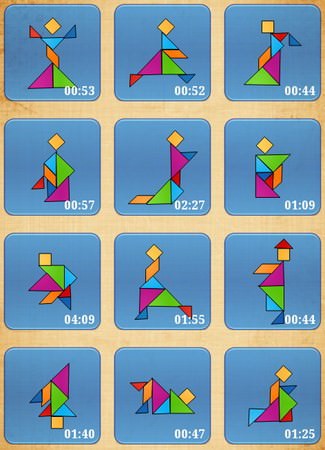
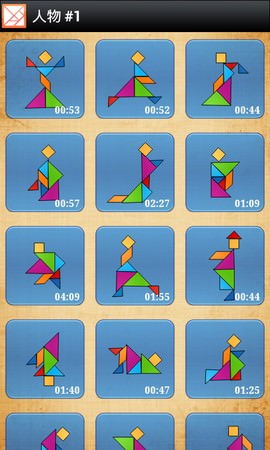
遊戲上大致依照拼出來的圖形,分成人物、動物、船隻、數字&字母、物品&建築、幾何形狀幾種,
還未解過的圖形會以陰影的圖示顯示,可隨意挑選關卡,
而解過得關卡則是會秀出怎麼拼成,花費多少時間等資料。
基本上就是要想辦法把七塊板子,拼成圖中要求的圖案,
而唯一需要翻面的板子則是(a)那塊,正方形在怎麼翻面還是正方形。
點某塊板子時,可以移動,也可以每45度的旋轉。
完成時則可以選擇重玩或下一關。
大師模式的關卡跟常規模式差不多,但….
大師模式則少了陰影的部份,
但是點提示(燈泡)依然會出現提示,可無限使用,
而解答(愛心)則是直接秀出答案,每一大關可以用10次。
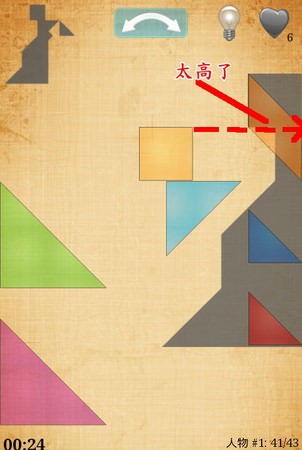
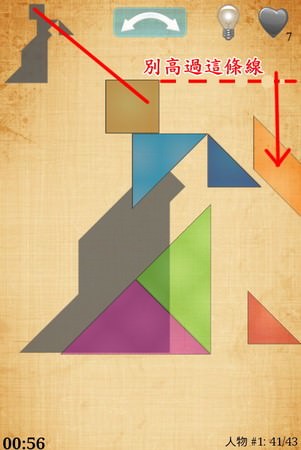
點燈泡時會短暫出現提示,這裡有個小技巧,
假設如上圖,你拼湊中的板塊,最上面那塊是正方形,那記得把其他版塊移到比這正方形還要低的位置,
這樣「陰影」跟「拼湊中的板塊」才會媒合。
左上圖為失敗例子,平行四邊形比最高的正方形還高了。
七巧板技巧
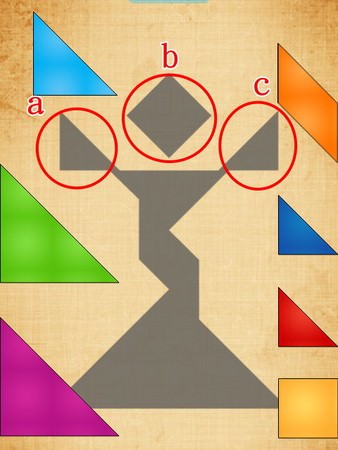
.先拼畸形地
像上圖,這種獨立的畸形地可以優先拼湊。
(a)(c)只有小三角形放的進去,可以最優先放;
雖然(b)可以用兩個小三角形來拼成,但這樣一來就沒版塊可以放(a)(c)了,所以絕對不可能是這樣放。
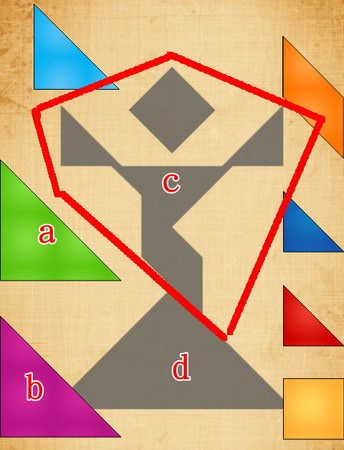
.先考慮最大與最小
如圖中(a)(b)兩塊,是不可能擠在(c)這一區,只有可能放在(d)這區,
我會優先放最大塊兩塊大三角形,正因為它大,所以可能的位置是比較有限的,
同時最小的小三角形、正方形也常常是可以最優先考量的。
.思考「不可能」
有時候,與其思考七巧板「怎樣可行」,
更多時候反倒是去思考「怎樣不可行」。
如上圖拼湊出這種不可能放置的現象(沒有那麼小的正方形),就知道淺藍色的中三角形一定是放錯位置了。
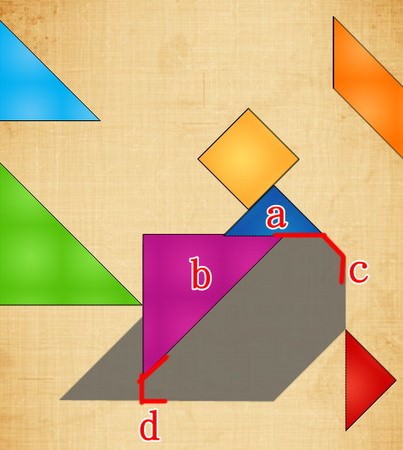
或是像這樣拼,乍看是沒什麼問題….
但如果延伸去思考,就不能會有能放在(c)跟(d)的板子,
這時就得考慮是(a)還是(b)放錯了,抑或是兩塊都錯了。
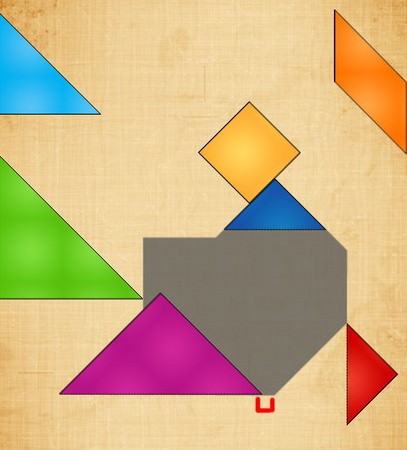
也有些很不明顯的,像是圖中這塊粉紅色大三角形放上去後,
雖然只跟邊邊差了0.2公分,薄的讓你感覺不到它的存在,
但這就表示這塊三角形一定放錯了。
.卡關時先玩別關
有時候人很容易有先入為主的「刻版印象」,玩遊戲也一樣,
會認為某個方塊就是一定要在那才行,這樣怎麼想也拼不出來,
這時不如放棄,先跳出去玩別關,到時候再回來玩這關,想法不一樣了,瞬間就能解開了。
人生也是這樣,往往你卡在某些點時,怎樣想就是在那鑽牛角尖,
但等過一段時間再來看,又會覺得那個問題不是問題了。
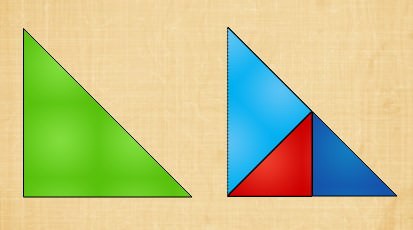
七巧板設計原理
七巧板的設計圖,可以發現是由一個大正方形所組成,
也可以從這看出不同板塊之間邊長的關係,像是正方形邊長 = 小三角形斜邊長,
兩個小三角形可以合出平行四邊形,
小三角形底邊長 = 平行四邊形長邊長,小三角形斜邊長 = 平行四邊形短邊長。
兩個小三角形可以合出正方形,
大三角形 = 2個中三角形 = 4個小三角形。
解題參考
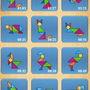
最後附上小豪解過的關卡給各位朋友參考一下,
僅供那種…您覺得「這怎麼可能拼的出這種形狀」時使用。XD
但還是建議…慢慢思考,沒有解不開的關卡,
一開始不習慣,總會多花點時間在嘗試,
後來習慣每塊板子的大小、邊長,很多時候甚至一看到影子,整個排法就會在腦袋中呈現了。
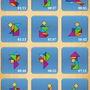
常規
 |
 |
 |
 |
 |
|
| 人物#1 | 1~12 | 13~24 | 25~36 | 37~48 | 49~60 |
 |
 |
 |
 |
 |
|
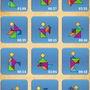
| 人物#2 | 1~12 | 13~24 | 25~36 | 37~48 | 49~60 |
 |
 |
||||
| 動物#1 | 1~12 | 13~24 | 25~36 | 37~48 | 49~60 |
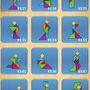
大師
 |
 |
 |
 |
|
| 人物#1 | 1~12 | 13~24 | 25~36 | 37~43 |
 |
 |
 |
 |
|
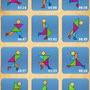
| 人物#2 | 1~12 | 13~24 | 25~36 | 37~38 |
 |
 |
|||
| 動物#1 | 1~12 | 13~24 | 25~36 | 37~46 |
在玩的時候我一直在想,
拼的快沒什麼,能想出這些圖案的人真是厲害呀!
延伸閱讀
.更多手機遊戲、手機app介紹:手機app、遊戲
.轉貼文章技巧:Facebook 轉貼連結的設定
.追蹤這個部落格的文章:闕小豪 on Facebook 或 Google+
如果您覺得寫得不錯,或是對您有幫助,請別客氣的留下回應或點個讚。
也歡迎各位朋友用「轉貼連結」或「分享」的方式轉貼文章,
請勿用複製全文的方式複製文章。